ロジカルシンキングとは何か【おすすめ本の紹介あり】

ここでは、ロジカルシンキングについて以下の観点で解説します。

• ロジカルシンキングとは
• ロジカルシンキングとクリティカルシンキングの違い
• 論理とは
• 論理関係と因果関係
• ロジカルシンキングの手法
• ロジカルシンキングの道具
• ロジカルシンキング 本の紹介

ロジカルシンキングとは

ロジカルシンキング、論理的思考とは、物事を筋道立てて考える方法のことです。
ロジカルシンキングがビジネスで使われるシーンは、主に

• 課題に対する適切な解決策を考える場面
• あるテーマについて複数の代替案を構造的に考える場面

で、これによって、説得力のあるプレゼンテーションを行うことができます。

ロジカルシンキングとクリティカルシンキングの違い

ロジカルシンキングと似たような考え方にクリティカルシンキングがあります。
クリティカルシンキング、批判的思考とは、自分が、主観や偏見（バイアス）に流されず、客観的に考えているか批判しながら思考を進めていく方法のことです。
クリティカルシンキングでは、物事の因果関係や論理関係を批判的に考えます。
例えば、売上が上がらなくなったという現象が起きたら、なぜ、そうなったのか物事の因果関係を批判的に考え、真の原因（真因）を見つけ、課題（イシュー）として設定します。
次に、その課題を解決する筋道（論理関係）を、批判的に考え、適切な解決策を探します。
このように、ロジカルシンキングは、クリティカルシンキングの１要素として位置づけることができます。
なお、物事の因果関係を分析することによって真の原因（真因）を見つける代表的な手法にシステム思考があります。
クリティカルシンキングに興味がある方は以下の動画をご覧ください。

論理とは

ここで、論理的思考の「論理」について押さえておきましょう。
先ほど、論理的思考とは、物事を筋道立てて考える方法、と説明しましたが、論理とは、この「筋道」のことです。
つまり、物事の間にある法則的な連関のことです。
※法則とは常に成り立つルールのことです。
もう少し、詳しく説明します。
正三角形は三角形である。
この主張は正しいでしょうか。
正しいですね。
それでは、
100は大きな数字である。
この主張は正しいでしょうか。
この場合、比較する対象によって正しいか正しくないかが決まってくるので判断できないですよね。
この「正三角形は三角形である」のように、正しいか（真）、正しくないか（偽）がはっきりと決まる主張のことを「命題」といいます。
ちなみに、
２＋３＝６
のように正しくない主張も命題です。
「論理」とは、命題の関係のことで、それによって組み立てられた体系を「理論」といいます。
数学や論理学でいう命題論理の場合、真偽の判断をするためには厳密な証明が必要ですが、世間一般で考える論理の場合、その真偽の判断に個人の価値観が入ることが多々あります。
ロジカルシンキングは、世間一般で考える論理も含めて考えます。
命題論理でよく使う関係としては、

• 「否定（¬）」
• 「かつ（∧）」「または（∨）」
• 「ならば（⇒）」

があります。
命題論理では、常に真になる命題を恒真命題（tautology：トートロジー）といい、代表的なものとして、以下の論理法則（ルール）があります。

• 排中律(law of the excluded middle)

P∨￢P
Pか￢Pのどちらかは真になる。
かならず真か偽かが定まる。
２値論理ともいい、「真でも偽でもない」という曖昧な状態は起こらない。
数学の論理では常に意識される。
つまり、「あたりまえ！」です。
よく、「あたりまえ！」と言いますが、そんな時は、排中律になっているか確認するようにしましょう。

• 矛盾律(law of contradiction)

￢（P∧￢P）
Pと￢Pの両方が真ということはあり得ない。
つまり、「あり得ない！」です。
よく、「あり得ない！」と言いますが、そんな時は、矛盾律になっているか確認するようにしましょう。

論理関係と因果関係

次に、「ならば（⇒）」について見ていきましょう。
P⇒Q（PならばQ）
という主張がある場合、Pを、その主張の仮定（premise）といい、Qを、その主張の結論（conclusion）といいます。
つまり、Pという仮定からQという結論が導かれるという主張です。
この
P⇒Q
が真になるのは、
「Pが真であるときは、必ずQも真である」
が成り立つときです。
それでは、Pが偽のときはどうかというと、
Pが偽のとき、P⇒Qは、Qの真偽にかかわらず常に真になります。
不思議ですよね。
真偽表で書くと以下のようになります。
※TはTrueで真、FはFalseで偽を表します。

例えば、次の例を考えてみましょう。
女子学生⇒女性
女子学生が真で、女性が真の場合、「女子学生であれば女性」ということで真ですよね。
女子学生が真で、女性が偽の場合、「女子学生だけど女性ではない」ということになり偽になります。
女子学生が偽で、女性が真の場合、「女子学生ではないけれど女性である」場合もあり得るので真ですよね。
女子学生が偽で、女性が偽の場合、「女子学生でも女性でもない」場合もあるので真になります。
※トランスジェンダーは考慮していません。
さて、真偽表を見ると
「P⇒QまたはQ⇒P」は常に真とはりトートロジーであることがわかります。
つまり、P⇒QかQ⇒Pのどちらかは必ず成り立つということになります。
ここで、因果関係について考えてみましょう。
Pが原因でQという結果が起こる場合を
P→Q
と記述すると、これを
P⇒Q
つまり、PならばQと考えてよいか考えてみましょう。
Pが起これば（真）、Qが起こる（真）
Pが起きなければ（偽）、Qも起きない（偽）
と考えば、因果関係も論理関係として考えることもできそうです。
また、Pが起きても（真）、Qは起きない（偽）は偽になるので両関係は一致します。
しかし、
Pが起きない場合でも（偽）、Qは起きる（真）
場合、論理関係は真ですが、Qの原因がPのみの場合、因果関係は偽になります。
また、P⇒QかQ⇒Pのどちらかは必ず成り立つルールは因果関係にも成立するかというと必ずしもそうではないと考えられます。
なので、厳密に考えると論理関係と因果関係はわけて考えた方がよさそうです。

必要条件と十分条件

ここで、必要条件と十分条件について説明します。
P⇒Q
が真であるとき

• QはPが成り立つための必要条件
• PはQが成り立つための十分条件

といいます。
QがPが成り立つための必要条件であるということは、
Pが真であるためにはQが真である必要がある
ということです。
また、PがQが成り立つための十分条件であるということは、
Pが真であれば十分Qは真である
ということです。
女子学生⇒女性の場合で考えてみましょう。
女子学生⇒女性が真である場合、
女子学生が真であるためには女性である必要がありますし、
女子学生が真であれば女性であることになるので、
女性であることは、女子学生であることの必要条件になりますし、
女子学生であることは、女性であることの十分条件になります。
なお、女性であるだけでは、女子学生であるとはいえないので、女性であることは、女子学生であることの十分条件にはなりません。
また、P⇒QでありQ⇒Pである場合、PはQの必要十分条件、QはPの必要十分条件といい、P⇔Qと書きます。
※⇔は同値といいます。
最後に、P⇒Qの否定と順番を考えて、先の真偽表を見てみましょう。

• P⇒Qの順番を入れ替えたQ⇒Pを、P⇒Qの逆（converse）といいます。
• P⇒Qを否定した¬P⇒¬Qを、P⇒Qの裏（inverse）といいます。
• P⇒Qを否定し、かつ、順番を入れ替えた¬Q⇒¬Pを、P⇒Qの対偶（contrapositive）といいます。

対偶¬Q⇒¬Pは元の命題P⇒Qと同値です。
P⇒Q ⇔ ¬Q⇒¬P
なので、P⇒Qを証明する場合、その対偶である¬Q⇒¬Pが真であることを示すという方法もあります。
それでは、¬（P⇒Q）と同値になるのはどのような場合でしょうか。
P⇒Qが真の場合、「Pが真であるときは、必ずQも真である」ということなので、その否定は、Pが真でかつQが偽の場合と同じです。
なので、¬（P⇒Q）と同値になるのはP∧¬Qです。
¬（P⇒Q）⇔ P∧¬Q
P⇒Qを証明するとき、P⇒Q ∧ ¬（P⇒Q）の矛盾律を利用して、¬（P⇒Q）が真であることの矛盾を示してP⇒Qが真であることを証明する方法を「背理法」といいますが、P∧¬Qを示すことで¬（P⇒Q）が真であること示すことができます。

ロジカルシンキングの手法

演繹法と帰納法

さて、ロジカルシンキングで論理展開する場合の代表的な手法に演繹法（えんえきほう）と帰納法（きのうほう）があります。
この２つは代表的な科学的方法（科学的アプローチ）でもあります。
演繹法（deduction）は、一般的・普遍的な法則を前提として、より個別的・特殊的な結論を導き出す方法のことです。
演繹法は、三段論法とも呼ばれ、観察事項に、一般的・普遍的な法則を適用して結論を導きます。

• 一般的法則：「人間はいつか死ぬ」
• 観察事項：「ソクラテスは人間である」
• 結論：「ソクラテスはいつか死ぬ」

はよくある三段論法の例です。
一方、帰納法（induction）は、個別的・特殊的な事例から一般的・普遍的な法則を導き出す方法のことです。
帰納法は、観察されるいくつかの事象の共通点に着目して一般的・普遍的な法則を導きます。

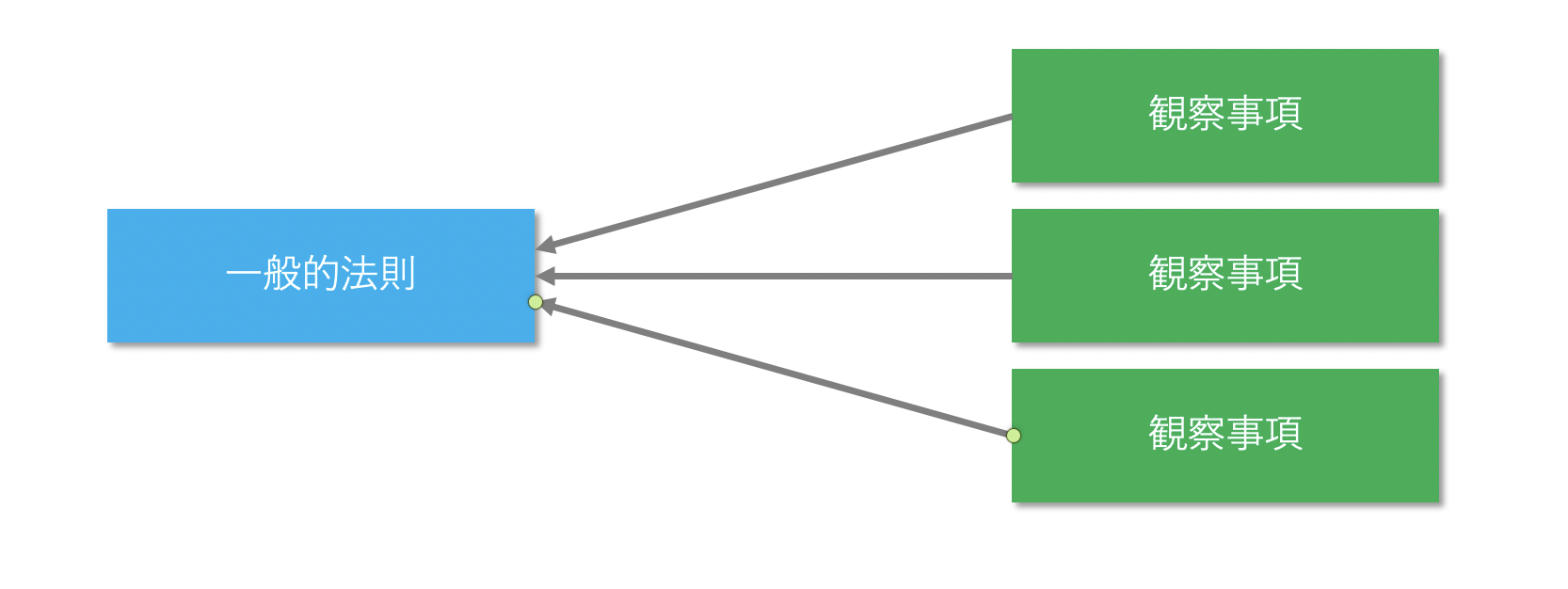
演繹法と帰納法の関係ですが、帰納法で導かれた一般的・普遍的な法則（真の場合）が演繹法に適用されます。

なお、演繹法の場合、数学で公理や定理から定理を導くように、前提となる一般的・普遍的な法則が真であれば、そこから導かれる結論も必然的に真になりますが（P⇒Q）、帰納法の場合、前提となる個別的・特殊的な事例が真であるからといって、そこから導かれる一般的・普遍的な法則が真である保証はありません。
一般的に帰納法の場合、結論の正しさが確率で表される蓋然性（がいぜんせい）の導出にとどまります。
つまり、演繹法の場合、法則に基づいた論理的推論に基づいて必然的な結論が導出されますが、帰納法の場合、事実に基づいた統計的推論に基づいて蓋然的な結論が導出されるいということです。
しかし、ある現象に関する理論が存在しない、あるいは、確実でない場合、演繹法は成立しませんが、帰納法は成立することができるので、帰納法は新しい分野を開発し、新しい理論を探索する場合、仮説を立てる方法として有効です。
自然科学や社会科学では、観察や実験が重視され、そこからさまざまな仮説が作られ、それがその分野の進歩の礎（いしずえ）となりますが、仮説を導くときの判断は常に帰納的に行われます。
※蓋然
ある程度確実であること。必然の反意語。

論理的推論

演繹と帰納に仮説推論を加え、論理的推論という観点で考えてみましょう。
論理的推論には、大きく以下の３つがあります。

• 演繹（Deduction）

演繹は、規則と前提から結論を導きます。
「A⇒B が成り立ち、かつ、Aが成り立つなら、Bが成り立つ」という三段論法です。
前提を原因、結論を結果と考えても良いでしょう。
また、規則とは、前提が真であれば結論も必ず真になるという論理的関係のことです。
数学者は、通常、演繹的に推論します。
演繹の場合、前提が真ならば結論も真になることを保証します。

• 帰納（Induction）

帰納は、前提が結論を伴ういくつかの事例を観察した結果として規則を推論します。
科学者は、通常、帰納的に推論します。
帰納の場合、推論した規則が真であることを保証しないので蓋然的、つまり、確率的な推論になります。

• 仮説推論（Abduction）

仮説推論は、結論に規則を当てはめて前提を推論します。
医者や探偵、コンサルタントは、通常、仮説推論をします。
仮説推論の場合、推論した前提が真であることを保証しないので蓋然的、つまり、確率的な推論になります。

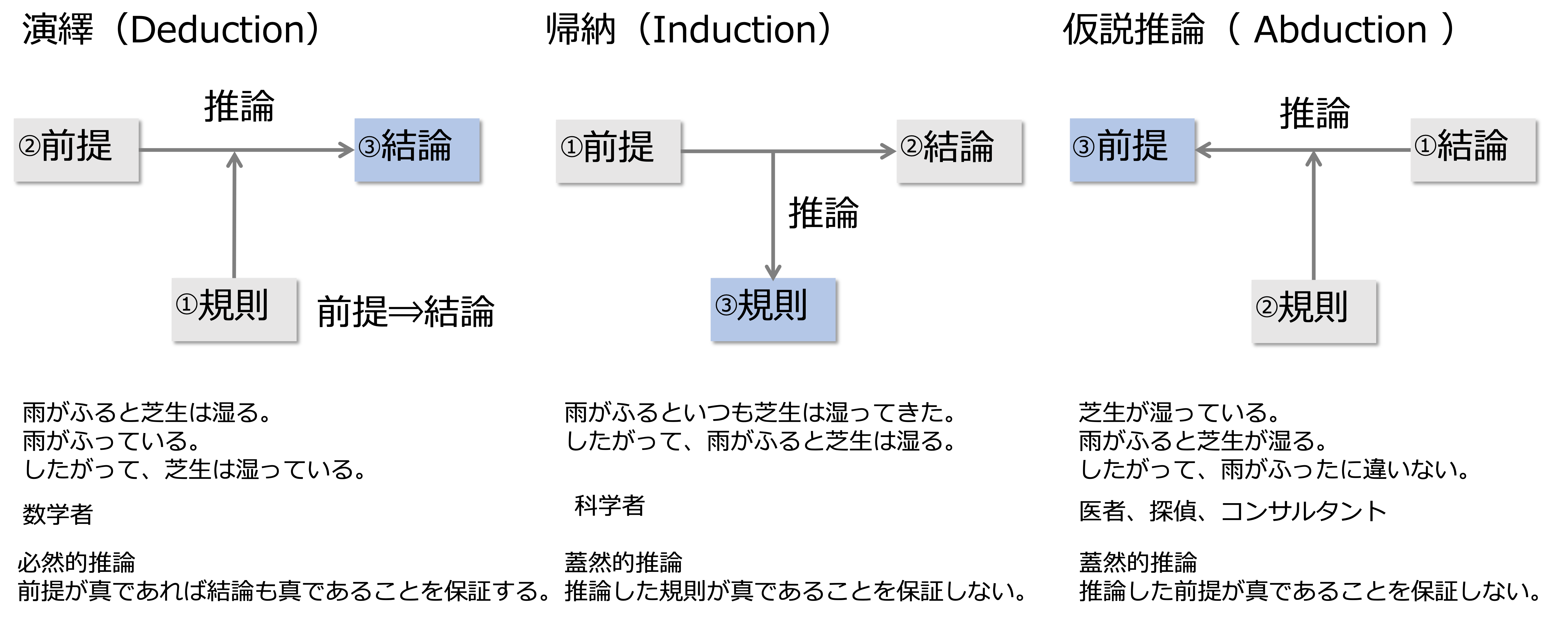
この３つの関係を問題を解決するプロセスで考えてみましょう。

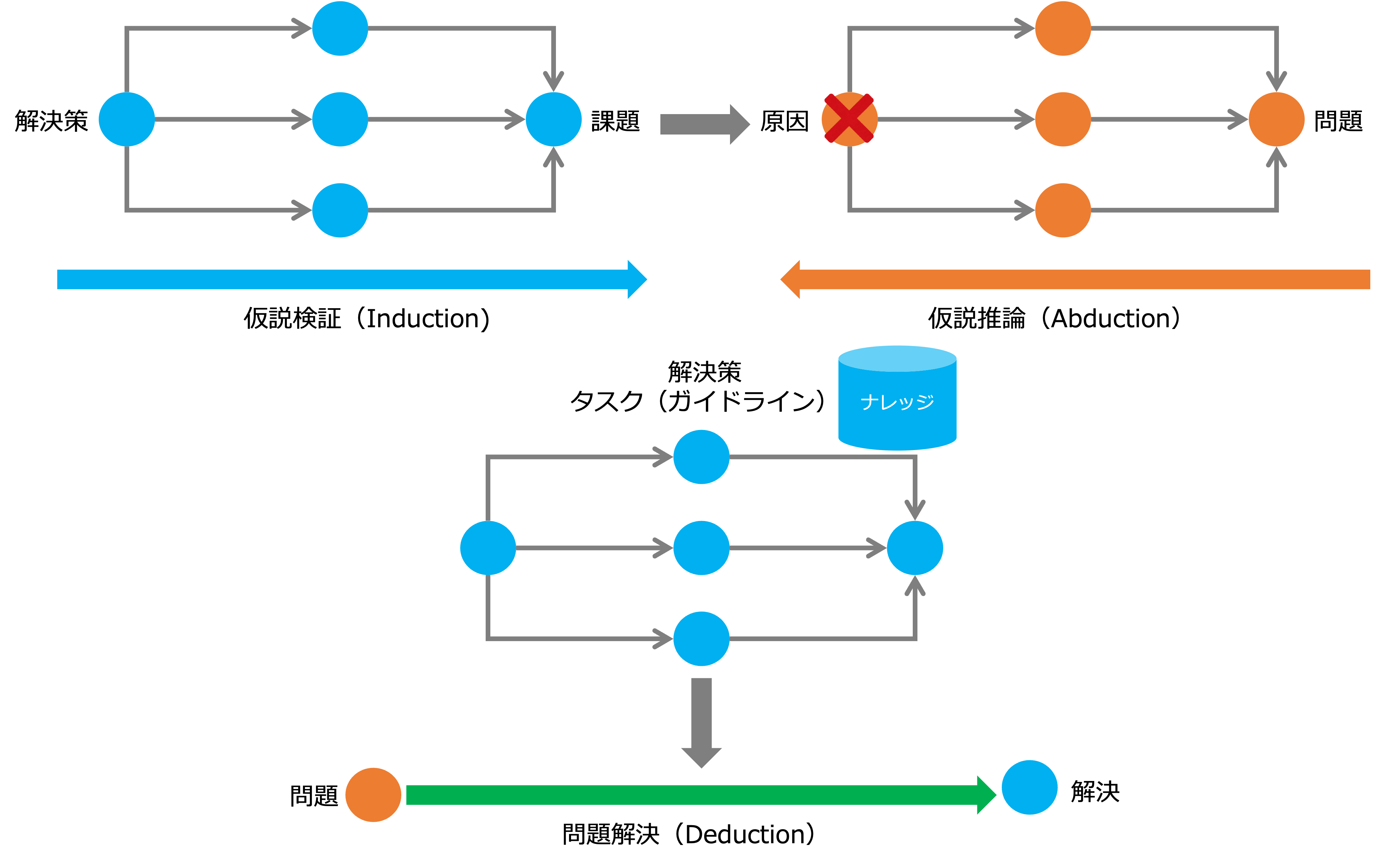
• なんらかの問題が生じた場合、仮説推論で、その原因を特定します。
  システム思考では、因果関係の型（パターン）を使って仮説推論します。
  デザイン思考では、人間、および、その集団を観察することで仮説推論します。
• 次に、原因を取り除くための課題を設定し、それを解決するための解決策（規則）を設計後、その確からしさを帰納的に検証します（仮説検証）。
• 最後に、検証された解決策を問題に適用して演繹的に問題を解決します。

なお、検証された解決策は、組織的なナレッジ（知的資産）になります。

科学的アプローチ

科学では、演繹的（Deductive）にモデル（解決策である規則）を考えて、帰納的（Inductive)に（実験により）、モデルを検証します。
モデル（数理モデル含む）は、システムを構成する要素を分析し、要素を組み合わせる（統合する）ことで創ることができます（分析・統合アプローチ）。

圏論

圏論（カテゴリー論）の圏（Category）は、対象（Object）と射（Morphism）から成っています。

論理関係や因果関係も、ある種の圏（Category）を形成します。

論理関係の圏（Category）が理論です。

なお、相関関係はあっても、それが因果関係であるとは限りません。

科学は、現象の法則をモデル化します。

物事の因果が絶え間なく続くとすれば、あるのは現象（射）であって実体（対象）はないことになります。

お釈迦様は、こころの現象を引き起こすエネルギーは渇愛であることを発見しました。
四聖諦とは何か

弁証法

演繹法、帰納法以外の論理展開の手法としてよく用いられるのが弁証法です。
前述した通り、命題論理には「Pと￢Pの両方が真ということはあり得ない」という矛盾律があります。
￢（P∧￢P）は常に真。
これに対して、弁証法は、矛盾を偽だとは決めつけず、物の対立・矛盾を通して、それらを統合することにより一層高い境地に進むという論理展開の方法です。
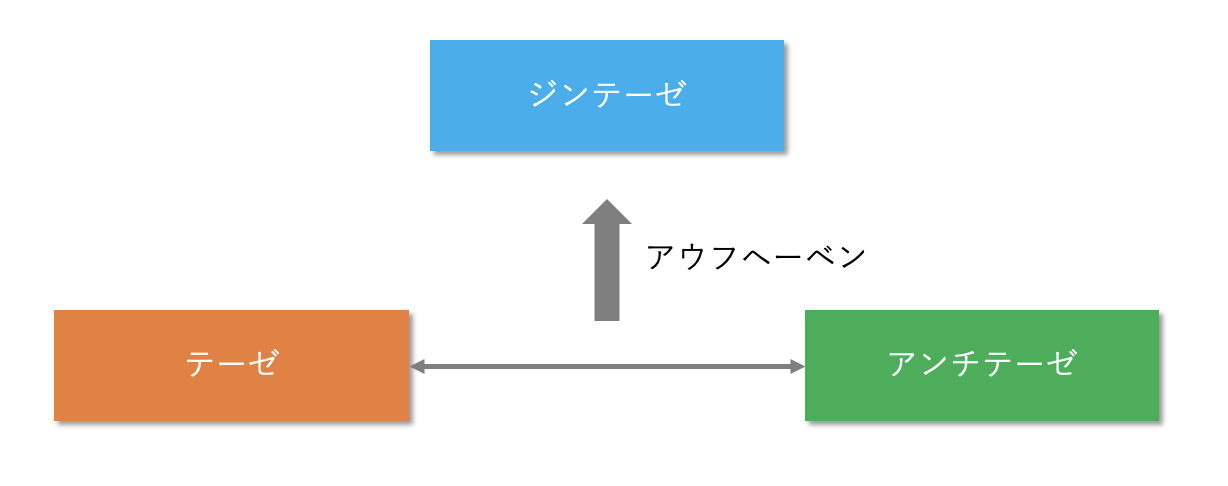
具体的には、ある真の命題（テーゼ）と、その反対である偽の命題（アンチテーゼ）があった場合、それらを統合することで、より次元の高い命題（ジンテーゼ）に進むという論理展開をします。
このとき、テーゼとアンチテーゼを統合する作用を「アウフヘーベン」といいます。

ロジカルシンキングの道具

ここで、ロジカルシンキングでよく使われる道具について紹介します。

• MECE（Mutually Exclusive and Collectively Exhaustive)

分析対象をグループ分けする際に、「モレなくダブりなく」行うべきであるということを示した考え方。
MECEをミッシー、あるいは、ミーシーと読みます。

• ピラミッドストラクチャー

結論と根拠を多段に組み立てることによって作られる構造のことです。
ドキュメントの骨子全体の構造を表現するに用いられます。

• ロジックツリー

問題の分析や、課題の整理の結果をツリー構造として表現したものです。

• フレームワーク

物事をMECEに整理するときに用いられる思考の枠組みのことです。
ビジネスに関する物事を分析するときによく使われます。

以上、ここでは、ロジカルシンキングの道具を４つ紹介しました。
なかでもMECE（モレなくダブりなく）は、他の道具の前提になるので重要です。

MECE

これはMECEのイメージを描いた図です。

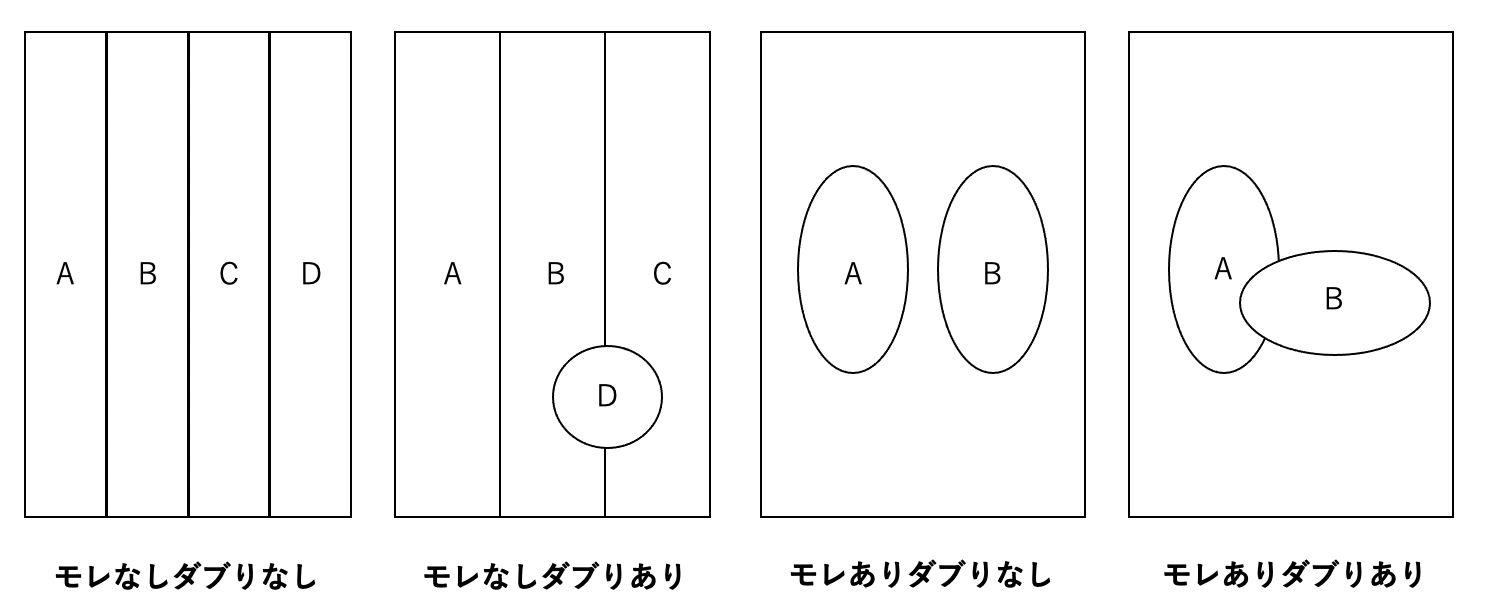
なぜ、分析対象を分類するとき「モレなくダブりなく」行うべきなのでしょうか。
例えば、事業戦略を考えてみましょう。
戦略というのは「戦（いくさ）」を「略（りゃく）」すと書くように、効率的に戦うための方策です。
企業は、限られた資源を最適な領域に投入しようとします。
例えば、市場を細分化してターゲットを絞り、そこに人、もの、金といった資源を集中的に投入します（選択と集中）。
この場合、市場をモレなくダブりなく分類する必要があります。
もし市場にモレがあった場合、どうなるでしょうか。
もし、モレた市場に、商品を購入してくれる重要顧客がいた場合、大変な機会損失になります。
次に、市場にダブりがあった場合、どうなるでしょうか。
この場合、同じタイプの市場に、同じだけ資源を投入することになるので、それだけ無駄が発生します。
このように、事業戦略という観点からもMECEはとても重要になります。

ロジカルシンキング 本の紹介

照屋華子・岡田恵子, 東洋経済新報社, 2001年
日本でロジカルシンキングが広まった契機になった本といわれています。

齋藤 嘉則, ダイヤモンド社, 1997年
ロジカルシンキングに関する記事によく引用される本です。

バーバラ・ミント, グロービスマネジメントインスティテュート, 1999年
こちらも、ロジカルシンキングに関する記事によく引用される本です。

以上、今回は、ロジカルシンキングについて解説しました。
動画でも解説しています。